Hello reader, welcome to my Know The Math series, a less formal series of blogs, where I take you through the notoriously complex backend mathematics which forms the soul for machine learning algorithms. I try and summarise works of famous researchers, put them as my notes and share with everyone in hopes that it might be helpful for you too!
This is in continuation to the last HMM mini-blog which covered the setup, the example in case and our variables. I am again going to try and summarise Jurafsky’s work over here, as quick notes!.
Before we begin, I need you to conduct a ceremony:
- Stand up in front of a mirror, and say it out aloud, “I am going to learn the Math behind HMM & the Viterbi Algorithm, today!”
- Take a out a naice register & pen to go through the derivation with me.
Contents
- Introduction
- The components of Hidden Markov Model
- First-Order HMM & its Assumptions
- 3 Fundamental problems of HMM
- Understanding the Case & Example
- The Forward Algorithm
- References
Introduction
Recalling from previous mini-blog on HMM, we know that our 2nd problem is to find the best Hidden state sequence Q when an input observation sequence and the Hidden Markov model λ are given. Building from the Eisner’s example (refer here), this means that let’s say, we have been given a sequence of 3-1-3 ice-creams on 3 consecutive days and our Hidden Markov model, what is the most probable sequence of hidden states?
The Viterbi Algorithm
Theoretically, we could apply the Forward algorithm for all possible hidden state sequences, and then simply take the maximum probability from the sequences. And the sequence which wil have the maximum likelihood will simply be our desired hidden state sequence as well. But, as we discussed in the last mini-blog, for N number of hidden states, if we carry out Forward algorithm for each, then the worst case complexity will reach O((TN^2) * (N^T)) which simplifies to O(N^T) and is essentially an exponential time algorithm. The Viterbi algorithm will help us solve the 2nd problem as mentioned above as well as the exponential time complexity issue we face. Like the Forward Algorithm, this too has a worst case time complexity of O(TN^2) optimised by Dynamic Programming. At each hidden state for every observation symbol in our sequence, we are simple going to select the hidden state which has the maximum probability amongst all paths from the very first symbol in observation sequence.
Seeing how we explore best path from all hidden sequences and the idea in Viterbi algorithm, source: Jurafsky’s work
In the algorithm, probability at every hidden state has been simplified as Viterbi Path Probability functions.
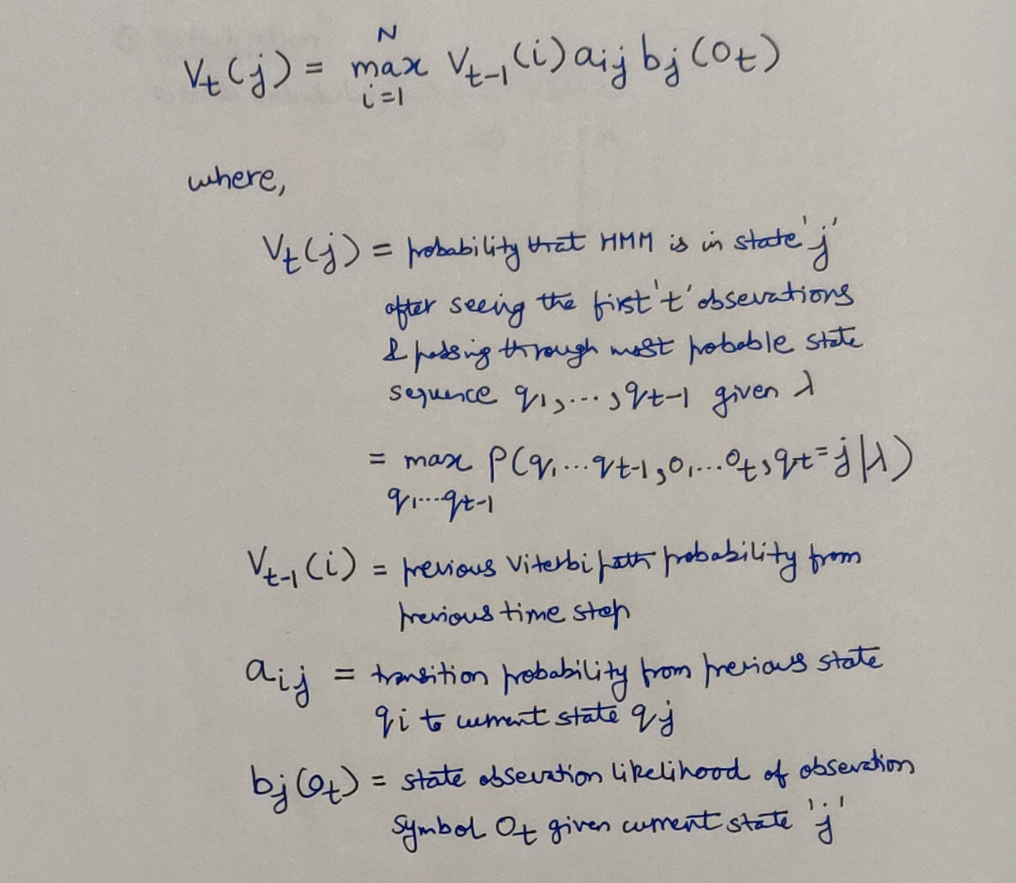The Viterbi Path probability, source: Jurafsky’s work
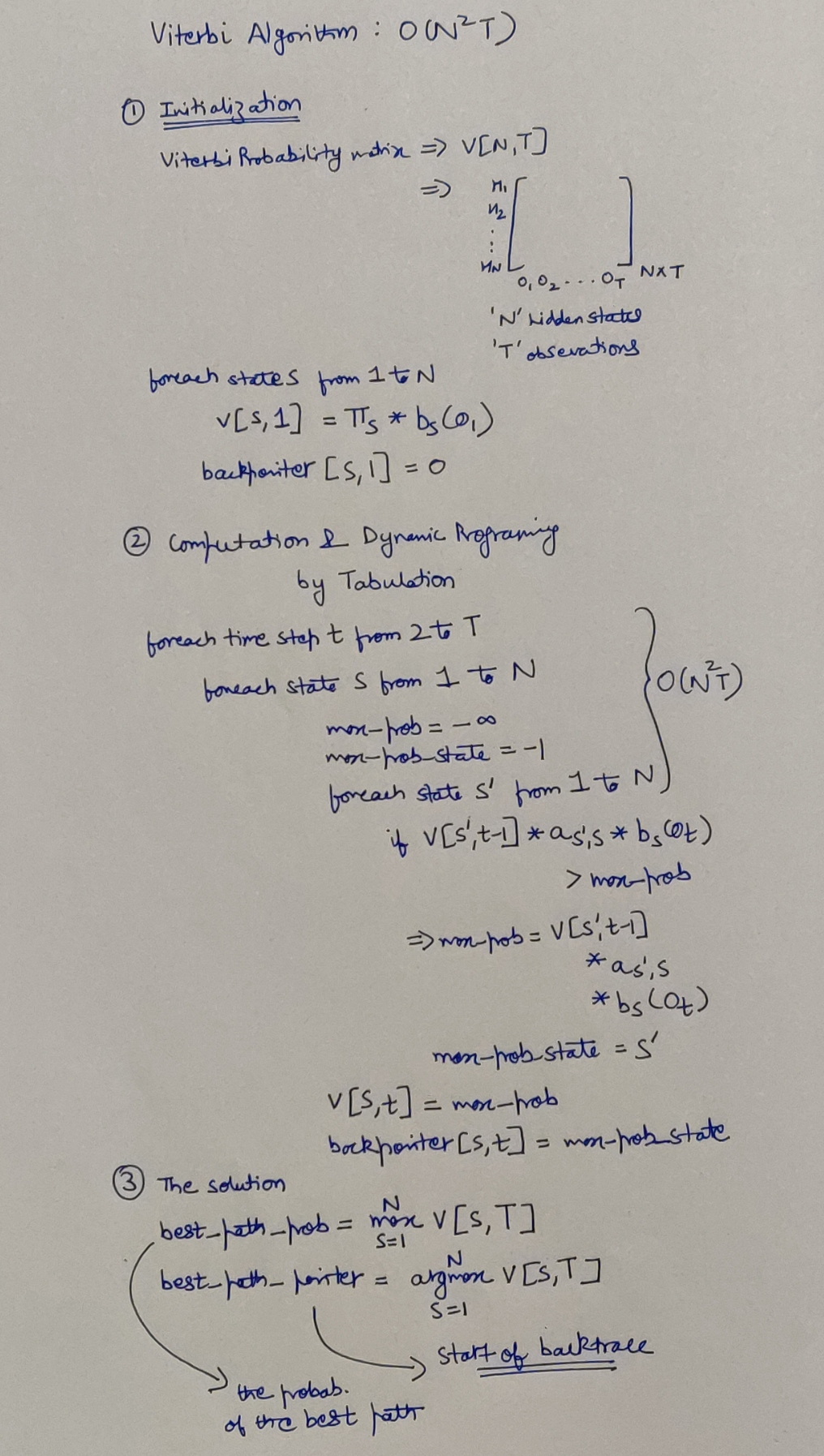Algorithm Pseudocode & Time Series Analysis
Hope I was able to help you out with the concepts mentioned! I would also request to have a look at the original work, since this is just a summarised version of it for quick revision. Thank you so much Professor Jurafsky for the pathbreaking work.
References
- https://web.stanford.edu/~jurafsky/slp3/A.pdf
- https://cs.jhu.edu/~jason/papers/eisner.tnlp02.pdf
- http://mlg.eng.cam.ac.uk/zoubin/papers/ijprai.pdf
- https://towardsdatascience.com/introduction-to-hidden-markov-models-cd2c93e6b781
प्रकृतेर्गुणसम्मूढ़ाः सज्जन्ते गुणकर्मसु ।
तानकृत्स्नविदो मन्दान्कृत्स्नविन्न विचालयेत् ॥
– Bhagavad Gita 3.29 ॥
(Read about this Shloka from the Bhagavad Gita here at http://sanskritslokas.com/)
Know The Math - The Hidden Markov Model & the Forward Algorithm