Hello reader, welcome to my Know The Math series, a less formal series of blogs, where I take you through the notoriously complex backend mathematics which forms the soul for machine learning algorithms. The idea for the series originated from my Project - NIFTYBANK Index Time series analysis, Prediction, Deep Learning & Bayesian Hyperparameter Optimization where people also asked to explain the underlying concepts.
co-author: Maharshi Parekh
Before we begin, I need you to conduct a ceremony:
- Stand up in front of a mirror, and say it out aloud, “I am going to learn the Math behind PCA, today!”
- Take a out a naice register & pen to go through the derivation with me.
Contents
Introduction
Recently, I finished this specialization on Coursera: Mathematics for Machine Learning and the instructor Professor Marc Peter Deisenroth along with others are exceptional in their teaching methods! My friend Maharshi found this book, Mathematics for Machine Learning online, from where we are borrowing most of the content in this short article. Here we are trying to breakdown the underlying math in a much verbose manner. I strongly recommend the course and the book for beginners out there.
So, before we begin, What is PCA? It’s a linear dimensionality reduction algorithm which we can use to operate on datasets which contain a large number of features. Because the more features we have, the better hardware+time+patience+modelling skills are required to operate on them. So basically, this is what is PCA will do for us in the most layman picture:
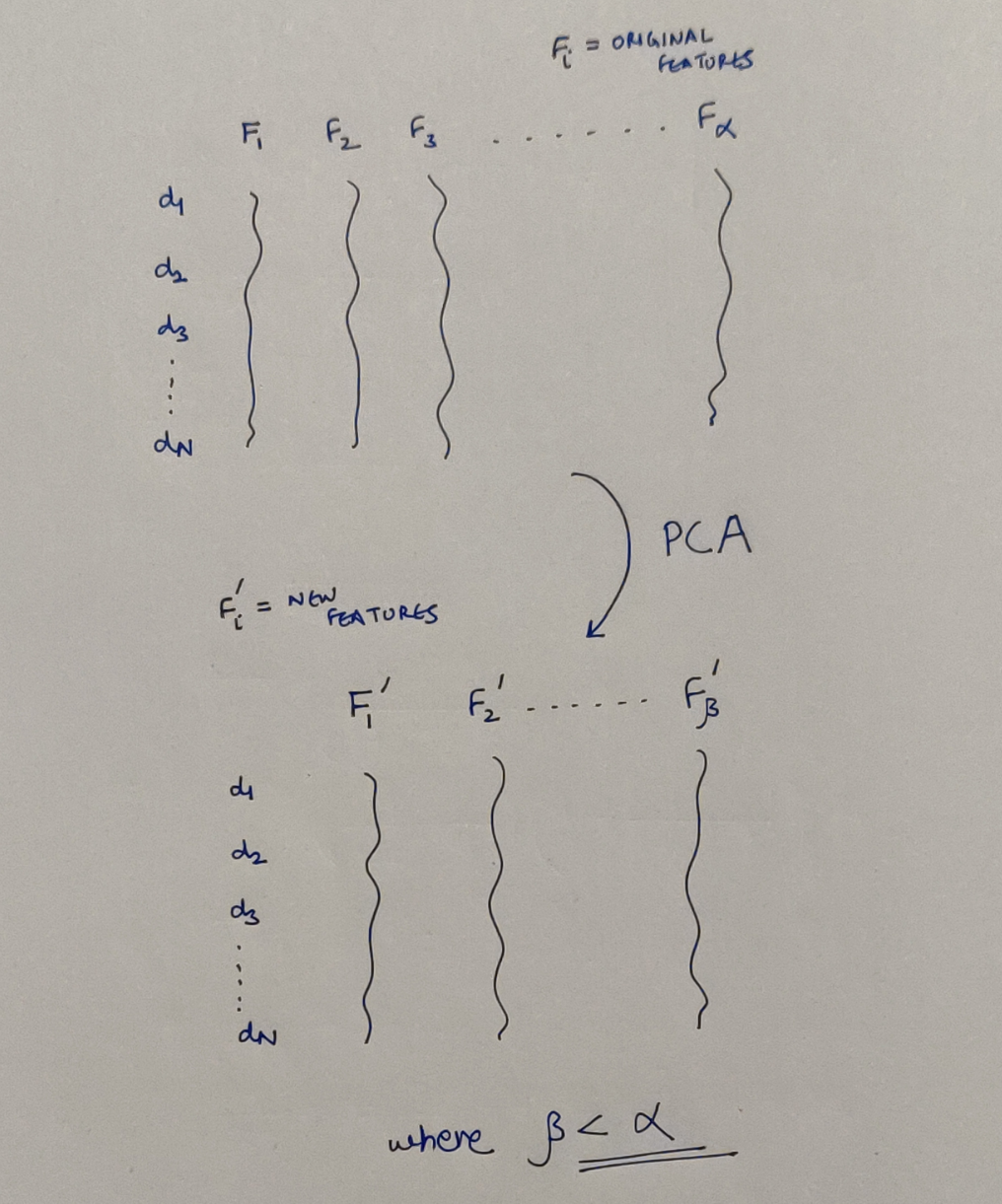 What PCA does!
What PCA does!
Now we’ll see as to how we achieve this and how we justify doing it. We’ll require some Linear Algebra, some calculus and some determination.
Let’s define our dataset and it’s variance-covariance matrix. Don’t fret about this matrix right now, it’s a weapon we’ll use later. We can see that each data point is represented as a D-dimensional vector and the data is centered i.e. the mean is 0.
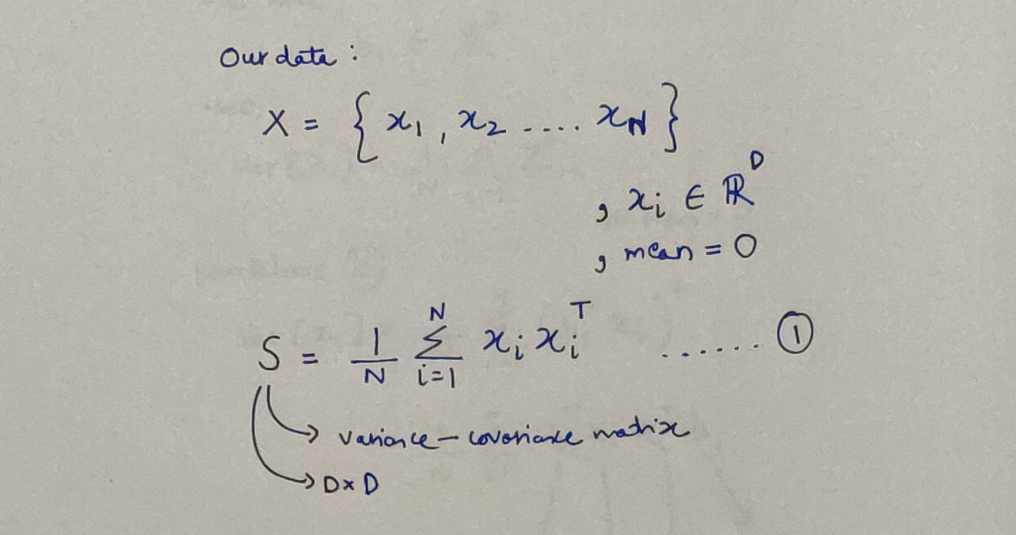 The given dataset
The given dataset
Some key assumptions & constraints
 Meet the constraints
Meet the constraints
Here we are trying to find a M-dimensional vector space which is a subset of the given vector space, such that the M < D; on which we will project our data. More mathematically, we are trying to find the set of Basis vectors B such that there is minimal loss of information due to compression from D dimensions to M dimensions, i.e. we have to capture the largest amount of variance from the original data in our lower dimensional projection.
The Derivation
We start by finding the first D x 1 dimensional vector b1 which will maximize the variance of the first co-ordinate Z1. REMEMBER: Each Z1i is the co-ordinate of the projection of Xi onto the 1-dimensional subspace spanned by b1.
 The Variance relation
The Variance relation
It is this variance, that we have to maximize subject to our constraints. And now, we are back again at the optimization stage. This time, we’ll use the Lagrangian Multiplier to conduct optimization.
 Using Lagrangian to Optimize
Using Lagrangian to Optimize
Alot has happened in this bit. Let’s talk about the GOLD first. This serves as motivation for the famous Characteristic polynomial. What it means is that b1 is an eigen vector of the variance-covariance matrix S, the Lambda is the corresponding eigen value. And using this result we have derived that our Variance has the value of this Lambda. And hence, to maximize it, we choose the vector associated with the largest eigen value from S.
Short Note
Remember, how we began with centered data? Turns out, without any loss of generality, we can assume that the data is centered. Let’s see how:
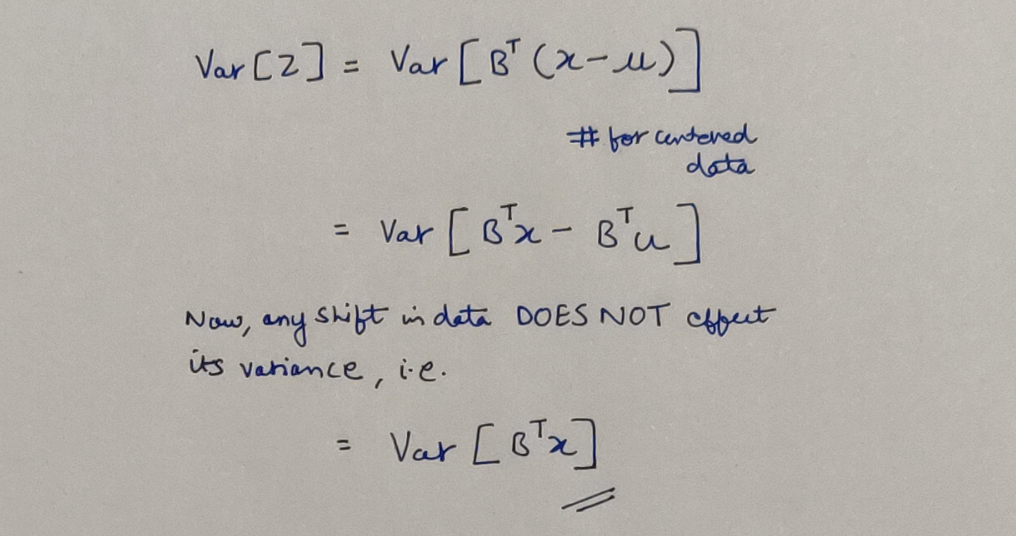 To center or not to center?!
To center or not to center?!
Hope I was able to help you out with the concepts mentioned! If not please leave feedback in comments as to how I can improve, since I plan to continue the Know The Math series. Thank you so much Professor Marc Peter Deisenroth for writing such an amazing book and publishing the course!
References
- https://mml-book.github.io/book/mml-book.pdf
- https://www.coursera.org/learn/linear-algebra-machine-learning/home/welcome
- https://www.cse.iitb.ac.in/~cs749/spr2017/handouts/lewis_pca_derivs.pdf
- https://courses.cs.ut.ee/MTAT.03.227/2014_spring/uploads/Main/lecture-notes-9.pdf
- https://www.stat.cmu.edu/~cshalizi/uADA/12/lectures/ch18.pdf
- http://alumni.media.mit.edu/~mkc/thesis/Appendix2.pdf
- https://datascienceplus.com/understanding-the-covariance-matrix/
- https://towardsdatascience.com/x%E1%B5%80x-covariance-correlation-and-cosine-matrices-d2230997fb7
एतां विभूतिं योगं च मम यो वेत्ति तत्त्वतः ।
सोऽविकम्पेन योगेन युज्यते नात्र संशयः ॥
– Bhagavad Gita 10.3 ॥
(Read about this Shloka from the Bhagavad Gita here at http://sanskritslokas.com/)
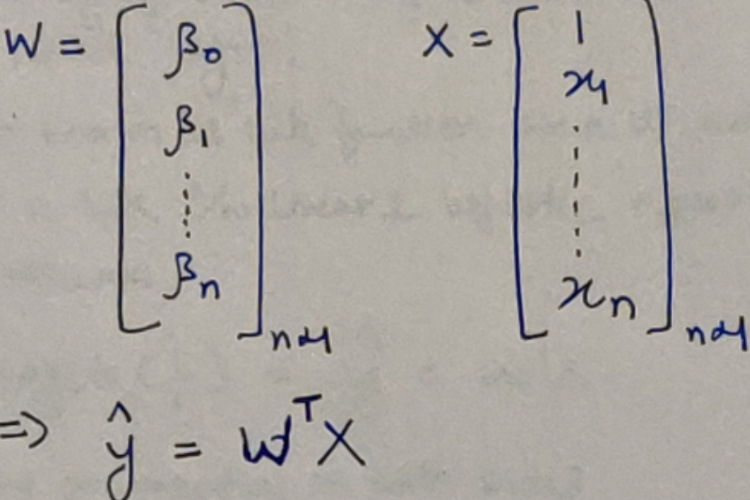 Know The Math - Everything Logistic Regression
Know The Math - Everything Logistic Regression